تناولنا، بالأقسام السابقة من هذا الفصل، جميع بُنَى التحكُّم (control structures) المُدعَّمة بلغة الجافا، ولكن قبل الانتقال إلى الفصل التالي، سنُلقِي نظرة مبدئية على موضوعين إِضافيين مُرتبطين نوعًا ما ببُنَى التحكُّم.
سنُلقِي في هذا القسم نظرة خاطفة على المصفوفات (arrays)، والتي تُعدّ واحدة من أكثر هياكل البيانات (data structure) شيوعًا. بالإضافة إلى ذلك، تَتطلَّب معالجة المصفوفات (array processing) اِستخدَام بُنَى التحكُّم، وهو ما سيمنحك الفرصة لتطبيق بعضًا مما تَعلَّمته عن بُنَى التحكُّم. سنتحدث في الفصل التالي عن الرسومات الحاسوبية (computer graphics)، والتي ستسمح لك أيضًا باستخدام بُنَى التحكُّم، ولكن بسياق مُختلِف نوعًا ما.
إنشاء المصفوفات واستخدامها
يتكون الهيكل البياني (data structure) من مجموعة من العناصر (items)، مُجمَّعة معًا بحيث يُمكِن التَعامُل معها كوحدة واحدة (unit). تُعدّ المصفوفة (array) هيكلًا بيانيًا (data structure)، تُرتَّب فيه العناصر كمتتالية مُرقَّمَة (numbered sequence)، بحيث يُمكِن الإشارة إلى كل عنصر مُفرد بها بواسطة رقم المَوْضِع (position number) خاصته. تَشترِط لغة الجافا -بخلاف بعض لغات البرمجة الأخرى- أن تكون جميع عناصر (items) المصفوفة من نفس النوع، كما يبدأ العدّ فيها دائمًا من الصفر. ستحتاج إلى التَعرُّف على عدة مصطلحات جديدة لتتمكَّن من الحديث عن المصفوفات: أولًا، طول/حجم المصفوفة (length/size of array) هو عدد العناصر (items) الموجودة بها، أما نوع المصفوفة الأساسي (base type of array) فهو نوع عناصرها المُفردة، وأخيرًا، فهرس العنصر (index) هو رقم المَوْضِع (position number) الخاص بالعنصر داخل المصفوفة.
لنفْترِض أنك تريد كتابة برنامج يُمكِنه معالجة الأسماء الخاصة بألف شخص، يَعنِي ذلك أنك في حاجة إلى طريقة للتَعامُل مع كل هذه البيانات. ربما ظننت -قبل تَعرُّفك على هيكل المصفوفة البياني (array)- أن البرنامج سيحتاج إلى ألف مُتَغيِّر ليَحمِل أسماء كل هذه الأشخاص، وأنك ربما ستحتاج إلى ألف تَعْليمَة طباعة كي تَتَمكَّن من طباعة كل هذه الأسماء. سيكون ذلك ضَرْبًا من العبث بكل تأكيد. تستطيع، في الواقع، وضع جميع الأسماء بمصفوفة (array)، يُمثِلها مُتَغيِّر وحيد يَحمِل قائمة الأسماء كاملة. في هذا المثال، لمّا كان هناك ألف اسم مفرد، فإن طول المصفوفة (length) سيُساوِي 1000. ولمّا كان كل عنصر بالمصفوفة من النوع String، فإن نوع المصفوفة الأساسي (base type) هو الصَنْف String. وأخيرًا، سيكون أول اسم داخل المصفوفة بالفهرس 0 (index)، بينما سيكون ثاني اسم بالفهرس 1، وهكذا حتى نَصِل إلى الاسم الأخير، والذي سيكون بالفهرس 999.
يُمكِن لنوع المصفوفة الأساسي (base type of array) أن يكون أي نوع مُدعَّم بلغة الجافا، ولكننا سنكتفي حاليًا بمعالجة المصفوفات التي إِمّا أن يكون نوعها الأساسي هو النوع String أو أن يكون واحدًا من الأنواع الأوَّليّة (primitive types) الثمانية. يُطلَق اسم مصفوفة الأعداد الصحيحة (array of ints) على المصفوفات التي يكون نوعها الأساسي هو int، بينما يُطلَق اسم مصفوفة السَلاسِل النصية (array of Strings) على المصفوفات التي يكون نوعها الأساسي هو String. مع ذلك، لا تُعدّ المصفوفة -إذا أردنا تَحرِي الدقة- قائمة من قيم الأعداد الصحيحة (integers) أو قيم السَلاسِل النصية (strings) أو حتى أيّ قيم اخرى، فمن الأفضل أن تُفكِر بها كقائمة من المُتَغيِّرات من النوع العددي int أو كقائمة من المُتَغيِّرات من النوع String أو من أي نوع آخر، فدائمًا ما يكون هناك خَلطًا (confusion) مُحتمَلًا بين اِستخدَام المُتَغيِّرات (variables) كاسم لمَوْضِع ما بالذاكرة (memory location)، واِستخدَامها كاسم للقيمة المُخزَّنة بهذا المَوْضِع. يُعامَل أي مَوْضِع (position) بالمصفوفة كمُتَغيِّر (variable)، فيُمكِن لهذا المَوْضِع أن يَحمِل قيمة من نوع معين (نوع المصفوفة الأساسي) مثلما يُمكِن لأيّ مُتَغيِّر أن يَحمِل قيمة، كما يُمكِن لتلك القيمة أن تَتغيَّر بأيّ وقت مثلما يُمكِن لقيمة أي مُتَغيِّر أن تَتغيَّر. عادة ما يُطلَق اسم عناصر المصفوفة (elements of array) على مجموعة المُتَغيِّرات المُفردة (individual variables) الموجودة بالمصفوفة وتُكَوِّنها إجمالًا.
عندما تُستخدَم مصفوفة ببرنامج ما، فيُمكِنك -كما ذَكَرت مُسْبَّقًا- الإشارة إليها ككل باِستخدَام مُتَغيِّر، لكنك عادةً ما ستحتاج إلى الإشارة إلى عناصر المصفوفة المُفردة (elements of array) من خلال اسم معين، والذي يَعتمِد على كُلًا من اسم المصفوفة ككل وفهرس (index) العنصر، فتكون صياغة (syntax) الاسم كالتالي namelist[7]، حيث namelist هو المُتَغيِّر الذي يُمثِل المصفوفة ككل، بينما يُشيِر namelist[7] إلى العنصر الموجود بالفهرس ٧ بتلك المصفوفة. أي يُستخدَم اسم المصفوفة متبوعًا بفهرس العنصر ضِمْن أقواس معقوفة (square brackets) [ ] للإشارة إلى هذا العنصر بتلك المصفوفة. يُعامَل اسم العنصر بهذه الصياغة كأي مُتَغيِّر آخر، فيمكنك أن تُسنِد قيمة إليه، أو أن تَطبَعه، أو أن تَستخدِمه بأيّ تعبير (expression).
تَحتوِي أيّ مصفوفة على مُتَغيِّر -نوعًا ما- يُمثِل طولها (length). فعلى سبيل المثال، إذا كان لديك مصفوفة namelist، فإنك تَستطيع اِستخدَام namelist.length للإشارة إلى طولها. ومع ذلك، لا يُمكِنك إسْنَاد (assign) قيمة إلى ذلك المُتَغيِّر؛ لأنه لا يُمكِن تَغْيِير طول المصفوفة.
يجب أولًا أن تُصَرِّح (declaration) عن مُتَغيِّر مصفوفة (array variable)؛ حتى تَتَمكَّن من اِستخدَامه للاشارة إلى مصفوفة معينة. تَتوفَّر أنواع المصفوفة (array types) لتَخْصِيص نوع تلك المُتَغيِّرات، وبشكل عام، فإن نوع مصفوفة معينة (array type) يتكون من نوع المصفوفة الأساسي (base type) متبوعًا بزوج من الأقواس المعقوفة (square brackets) الفارغة. فمثلًا، يكون مُتَغيِّر مصفوفة (array variable) من النوع String[] في حالة إشارته إلى مصفوفة سَلاسِل نصية (array of Strings)، بينما يكون من النوع int[] في حالة إشارته إلى مصفوفة أعداد صحيحة (array of ints). اُنظر المثال التالي:
String[] namelist; int[] A; double[] prices;
يُمكِن للمُتَغيِّرات المُصرَّح عنها بتلك الطريقة الإشارة إلى المصفوفات، لكن لاحِظ أن مُجرَّد التَّصْريح عن المُتَغيِّر (variable declaration) لا يَتسبَّب بالإنشاء الفعليّ للمصفوفة. ينبغي إِسْناد قيمة لمُتَغيِّر المصفوفة (array variable) قبل اِستخدَامه -مثلما هو الحال مع جميع المُتَغيِّرات-، وفي هذه الحالة، تكون القيمة عبارة عن مصفوفة. تَتوفَّر صياغة خاصة (special syntax) للإِنشاء الفعليّ للمصفوفة؛ وذلك لأن المصفوفات -بلغة الجافا- هي بالأساس كائنات (objects)، وهو ما سنؤجل الحديث عنه؛ فهو غَيْر ذي صلة هنا. إجمالًا، يُستخدَم العَامِل new لإنشاء المصفوفات، انظر الأمثلة التالية:
namelist = new String[1000]; A = new int[5]; prices = new double[100];
تكون الصياغة كالتالي:
<array-variable> = new <base-type>[<array-length>];
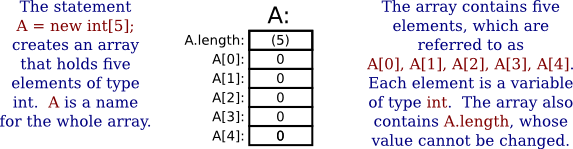
يُمكِن اِستخدَام عدد صحيح (integer) أو تعبير من النوع العددي (integer-valued expression) لتَحْدِيد طول المصفوفة A = new int[5];، أَصبح المُتَغيِّر A يُشير إلى مصفوفة مُكوَّنة من ٥ عناصر (elements) من النوع العددي (integer)، هي A[0] و A[1] و A[2] و A[3] و A[4]، كما أصبح A.length يَحمِل القيمة ٥.
اُنظر الصورة التالية:
عند إِنشاء مصفوفة أعداد صحيحة (array of int)، تُهيَئ (initialized) جميع عناصر المصفوفة أُتوماتيكيًا بحيث تَحمِل القيمة صفر، مما يَعنِي أن قيم جميع عناصر أيّ مصفوفة أعداد تكون مُساوِية للصفر بمُجرَّد إِنشاؤها. في المقابل، تَحمِل جميع عناصر أيّ مصفوفة قيم منطقية (array of boolean) القيمة المنطقية false بمُجرَّد إِنشاؤها. أمّا عناصر أيّ مصفوفة محارف (array of char) فتحتوي على المحرف المقابل لقيمة ترميز اليونيكود (Unicode code) رقم صفر \u0000 بمُجرَّد إِنشاؤها. وأخيرًا، فإن القيمة المبدئية لعناصر أيّ مصفوفة سَلاسِل نصية (array of String) تكون القيمة الفارغة null (تُستخدَم تلك القيمة مع الكائنات [objects] ولن نتَعرَّض لها حتى القسم ٥.١ لاحقًا).
المصفوفات وحلقات التكرار For
تُعدّ إِمكانية اِستخدَام مُتَغيِّر من النوع العددي (integer) أو حتى اِستخدَام تعبير من النوع العددي (integer-valued expression) كفهرس للعنصر (index of an element) واحدة من أهم مميزات المصفوفات. فعلى سبيل المثال، إذا كان لديك مصفوفة list، ومُتَغيِّر من النوع العددي الصحيح i، فبإمكانك اِستخدَام list أو حتى list[2*i+1] كأسماء مُتَغيِّرات، بحيث تُؤثِر قيمة i على ما يُشيِر إليه المُتَغيِّر فعليًا. يُساعدك ذلك في حالة أردت إِجراء معالجة معينة على جميع عناصر المصفوفة؛ حيث ستستطيع القيام بذلك ضِمْن حَلْقة التَكْرار for. فمثلًا، لطباعة جميع عناصر المصفوفة list، يُمكننا كتابة الآتي:
int i; // فهرس المصفوفة for (i = 0; i < list.length; i++) { System.out.println( list[i] ); }
في أول مرة تُنْفَّذ فيها الحَلْقة (loop) -أيّ خلال أول تَكْرار (iteration)-، ستكون قيمة i مُساوِية للصفر، أيّ سيُشيِر list إلى list[0]، ولذا تُطبَع القيمة المُخزَّنة بالمُتَغيِّر list[0]. في المرة الثانية، ستكون قيمة i مُساوِية للواحد، ولذا تُطبَع القيمة المُخزَّنة بالمُتَغيِّر list[1]. لمّا كان طول المصفوفة list يُساوِي ٥، فستنتهي حَلْقة التَكْرار (loop) بعد طباعة قيمة المُتَغيِّر list[4]؛ لأن قيمة i ستُصبِح مُساوِية للقيمة ٥، مما يَعنِي أن الشَّرْط الاستمراري (continuation condition) للحلقة i < list.length لم يَعُدْ مُتحقِّقًا بَعْد الآن. لاحِظ أن الشيفرة بالأعلى تُعدّ مثالًا نموذجيًا لاِستخدَام حَلْقة تَكْرار بغرض معالجة مصفوفة.
لنفْحَص عدة أمثلة اخرى، بفَرْض أن A هي مصفوفة أعداد حقيقية (array of double)، وكنا نُريد حِسَاب قيمة متوسط (average) جميع عناصر تلك المصفوفة. يُمكِننا ببساطة اِستخدَام حَلْقة التَكْرار for لحِسَاب حاصل مجموع الأعداد، ومِنْ ثَمَّ نُقسمها على طول المصفوفة، كالتالي:
double total; // حاصل مجموع الأعداد بالمصفوفة double average; // قيمة متوسط الأعداد int i; // فهرس المصفوفة total = 0; for ( i = 0; i < A.length; i++ ) { // أضف قيمة العنصر برقم الموضع i إلى حاصل المجموع total = total + A[i]; } average = total / A.length; // A.length هي عدد العناصر
مِثال آخر هو محاولة إِيجاد أكبر عَدَد بالمصفوفة A من المثال السابق. سنُنشِئ مُتَغيِّر max، بحيث نُخزِن فيه قيمة أكبر عَدَد مرَّرنا به حتى الآن، ثم سنبدأ بالمرور على جميع عناصر المصفوفة، وأينما وَجدنا عَدَد أكبر من قيمة المُتَغيِّر max الحالية، فإننا سنُسنِد ذلك العَدَد إلى المُتَغيِّر max. بعد الانتهاء من معالجة المصفوفة بالكامل، سيَحتوِي المُتَغيِّر max حتمًا على أكبر عدد داخل المصفوفة ككل. ولكن يَبقى السؤال التالي، ما هي القيمة الأوَّليّة للمُتَغيِّر max؟ ربما ببساطة نَستخدِم قيمة أول عنصر بالمصفوفة، أي A[0]، للتهيئة المبدئية للمُتَغيِّر max، ومِنْ ثَمَّ نبدأ عملية البحث عن قيمة أكبر منها بباقي عناصر المصفوفة، أي بدءً من العنصر A[1]:
double max; // اكبر عدد حتى الآن max = A[0]; // في البداية، أكبر عدد هو قيمة العنصر A[0] int i; for ( i = 1; i < A.length; i++ ) { if (A[i] > max) { max = A[i]; } } // بالوصول إلى تلك النقطة، يحتوي max على قيمة أكبر عدد
قد تَحتاج أحيانًا إلى معالجة بعض عناصر المصفوفة (elements of the array) وليس كلها. تُستخدَم تَعْليمَة if، في هذه الحالة، بداخل حَلْقة التَكْرار for لتَحْدِيد ما إذا كُنت تُريد معالجة العنصر الحالي أم لا. دعنا نُلقِي نظرة أخرى على مسألة حِسَاب قيمة متوسط (average) عناصر مصفوفة معينة، ولكن في هذه المرة، لنفْترِض أننا نُريد حِسَاب قيمة المتوسط فقط للعناصر غَيْر الصفرية (non-zero elements)، أيّ التي لا تحتوي على القيمة صفر. في هذه الحالة، قد يكون عدد تلك العناصر أقل من طول المصفوفة (length)، ولهذا سنحتاج إلى عدّ العناصر غَيْر الصفرية، والتي أُضيفت فعليًا لحاصل المجموع بدلًا من الاعتماد على طول المصفوفة. انظر الشيفرة التالية:
double total; // حاصل مجموع الأعداد غير الصفرية بالمصفوفة int count; // عدد الأعداد غير الصفرية double average; // متوسط الأعداد غير الصفرية int i; total = 0; count = 0; for ( i = 0; i < A.length; i++ ) { if ( A[i] != 0 ) { total = total + A[i]; // أضف قيمة العنصر إلى حاصل المجموع count = count + 1; // أزد قيمة العداد } } if (count == 0) { System.out.println("There were no non-zero elements."); } else { average = total / count; // اِقسم حاصل المجموع على عدد العناصر System.out.printf("Average of %d elements is %1.5g%n", count, average); }
الجلب العشوائي (Random Access)
اِستخدَمت جميع أمثلة معالجة المصفوفات -التي فَحْصناها حتى الآن- الجَلْب المُتتالي (sequential access)، أي عُولَجت عناصر المصفوفة (elements of the array) بنفس ترتيب حُدُوثها بالمصفوفة واحدًا تلو الآخر. مع ذلك، يُعدّ الجَلْب العشوائي (random access) واحدًا من أهم مميزات المصفوفات، حيث تستطيع الولوج لقيمة أيّ عنصر بالمصفوفة بأيّ وقت وبنفس الكفاءة وعلى قَدَم المُساواة.
دعنا نُلقِي نظرة على إِحدى المسائل المشهورة والمعروفة باِسم مُعْضِلة يوم الميلاد (birthday problem). بفَرْض وجود مجموعة من الأشخاص داخل حجرة، وليَكُن عَدَدهم هو N، فما هي احتمالية أن يكون لاثنين من هؤلاء الأشخاص نفس يوم الميلاد؟ (بمعنى أنهما قد وُلدَا بنفس اليوم، والشهر، ولكن ليس ضروريًا ولادتهما بنفس العام). يُقَلِّل غالبية الناس من شأن هذه الاحتمالية بشدة. سنَفْحَص، في الواقع، نسخة أخرى شبيهة من نفس السؤال: بفَرْض اختيارك لمجموعة أشخاص بشكل عشوائي، بحيث تَفْحَص يوم ميلادهم، فكم عَدَد الأشخاص الذين ستحتاج إلى فَحْص يوم ميلادهم قبلما تَجِد اثنين لهما نفس يوم الميلاد؟ تَعتمِد الإجابة على مِثل هذا السؤال على عدة عوامل عشوائية بالتأكيد، ولكن مع ذلك، يُمكِننا مُحاكاة هذه التجربة باِستخدَام برنامج، بحيث نُنْفِّذه عدة مرات، وهو ما سيُعْطِينا مُؤِشرًا تقريبيًا لعدد هؤلاء الأشخاص.
لمُحاكاة هذه التجربة، سنحتاج إلى معرفة جميع أيام الميلاد التي قد وَجدناها حتى الآن. لمّا كان هناك ٣٦٥ يوم ميلاد مُحتمَل (سنتجاهل الأعوام الكبيسة [leap years])، فإننا سنُنشِئ مصفوفة قيم منطقية (array of boolean) طولها (length) يُساوِي ٣٦٥، بحيث يُناظِر كل عنصر فيها يوم ميلاد مُختلِف، ويُعْلِمنا إذا ما كُنا قد وَجدنا شخصًا بنفس يوم الميلاد المُناظِر للعنصر أم لا. اُنظر الشيفرة التالية:
boolean[] used; used = new boolean[365];
بدايةً، ستُرقَّم أيام العام من ٠ إلى ٣٦٤، بحيث يُحدِّد المُتَغيِّر used -من النوع المنطقي- ما إذا سبق وأن وَجدنا شخصًا يوم ميلاده هو رقم اليوم (day number) i أم لا، مما يَعنِي أنه سيَحمِل القيمة المنطقية true في تلك الحالة. مبدئيًا، ستكون جميع قيم عناصر المصفوفة used مُساوِية للقيمة المنطقية false، وهو في الواقع ما يَحدُث أتوماتيكيًا عند إِنشاء المصفوفة. عند اختيارنا لشخص ما، يوم ميلاده هو رقم اليوم i، فإننا سنَفْحَص أولًا قيمة المُتَغيِّر used، فإذا كانت مُساوِية للقيمة المنطقية true، سيَعنِي ذلك أننا قد وَجدنا الشخص الثاني بنفس يوم الميلاد، ومِنْ ثَمَّ فإننا قد انتهينا. أمّا إذا كانت قيمته مُساوِية للقيمة المنطقية false، فسنَضبُط قيمة المُتَغيِّر used إلى القيمة المنطقية true، للإشارة إلى كَوْننا قد وجدنا الشخص الأول بيوم الميلاد ذاك. بَعْد ذلك، سنستمر بتَّنْفيذ البرنامج، فنختار الشخص التالي. اُنظر البرنامج بالأسفل (لاحِظ أننا لم نُحاكِي الأشخاص، فقط أيام الميلاد):
public class BirthdayProblem { public static void main(String[] args) { // لتخزين أيام الميلاد التي وجدنا أشخاص ولدوا بها boolean[] used; // عدد الأشخاص الذين تم فحص أيام ميلادهم int count; // القيمة المبدئية لجميع العناصر هي false used = new boolean[365]; count = 0; while (true) { // اختر يوم ميلاد بصورة عشوائية من صفر وحتى 364 int birthday; // يوم الميلاد المختار birthday = (int)(Math.random()*365); count++; System.out.printf("Person %d has birthday number %d%n", count, birthday); if ( used[birthday] ) { // وجدنا يوم الميلاد هذا من قبل، انتهينا break; } used[birthday] = true; } // نهاية while System.out.println(); System.out.println("A duplicate birthday was found after " + count + " tries."); } } // نهاية الصنف BirthdayProblem
ينبغي عليك أن تَقضِي بعض الوقت لدراسة البرنامج بالأعلى؛ وذلك حتى تَفهَم طريقة عمله، وطريقة اِستخدَامه للمصفوفة. شَغِّله أيضًا! ستكتشف أن احتمالية تَكْرار أيام الميلاد ربما هي أكبر مما كنت تَتوقَّع.
المصفوفات الممتلئة جزئيًا (Partially Full)
لنفْترِض أن لدينا تطبيقًا، بحيث يتغَيَّر -أثناء تَّنْفيذه- عَدَد العناصر المطلوب تخزينها بمصفوفة ما. لمّا كان من غَيْر المُمكن تَغْيِير طول/حجم (length/size) المصفوفة، كان لابُدّ لنا من اِستخدَام مُتَغيِّر مُنفصل لعدّ المَواضِع المُستخدَمة فعليًا بالمصفوفة. (تَحتوِي بالطبع جميع المَواضِع بأيّ مصفوفة على قيمة ما، ولكن ما يُهِمّنا هو عَدَد المَواضِع التي تَحتوِي على عناصر صالحة ومفيدة).
على سبيل المثال، يَقرأ برنامج ما الأعداد الصحيحة الموجبة (positive integers)، المُدْخَلة مِنْ قِبَل المُستخدِم، بحيث يَتوقَف البرنامج عن القراءة عند إِدْخَال عدد أقل من أو يُساوِي الصفر. يحتاج البرنامج لتَخْزِين الأعداد المُدْخَلة بهدف مُعالجتها لاحقًا (later processing)، ولذلك فإنه يَحتفِظ بها داخل مصفوفة من النوع int[]، هي المصفوفة numbers. بفَرْض أنه لن يتمّ إِدْخَال أكثر من ١٠٠ عدد، فإن حجم (length/size) تلك المصفوفة سيكون ١٠٠. نحتاج الآن إلى الإجابة على السؤال التالي: عند إضافة قيمة عنصر (member) جديد بالمصفوفة، بأيّ مَوْضِع سنضعه تحديدًا؟ للإجابة على هذا السؤال، سنحتاج إلى معرفة عَدَد الأعداد التي تمّ فعليًا قرائتها وتَخْزِينها بالمصفوفة، أيّ عَدَد المَواضِع المُستخدَمة فعليًا بالمصفوفة، ولهذا سنَستخدِم مُتَغيِّر من النوع العددي (integer)، وليَكُن المُتَغيِّر count. سيَعمَل هذا المُتَغيِّر كعَدَّاد (counter)، أيّ أننا سنزيد قيمة هذا المُتَغيِّر بمقدار الواحد في كل مرة نُخزِّن فيها عدد جديد بالمصفوفة. الآن، لمّا كان العدد الفعليّ للعناصر يُساوي قيمة المُتَغيِّر count، فلابُدّ أن تلك العناصر مُخزَّنة بالأرقام المَوْضِعية (position numbers) ٠، ١، …، وحتى count - 1، ولذلك فإن رقم المَوْضِع (position number) المتاح التالي هو قيمة المُتَغيِّر count. وعليه، فإن هذا هو المَوْضِع الذي سنُخزِّن فيه العنصر الجديد.
مثال آخر هو برنامج يَقرأ الأعداد المُدْخَلة من قِبَل المُستخدِم، وبحيث يَتوقَف عن القراءة عند إِدْخَال عدد يُساوِي الصفر. الهدف من البرنامج هو طباعة تلك الأعداد بترتيب مُعاكِس (reverse order) للترتيب الأصلي الذي أُدْخلت به. قد يبدو هذا المثال سخيفًا نوعًا ما، ولكنه على الأقل يَتطلَّب أن تكون الأعداد مُخزَّنة بمصفوفة، بعكس أنواع آخرى كثيرة من المعالَجات، والتي يُمكِن إِجراؤها دون الحاجة إلى الاِحتفاظ بقيم الأعداد المُفردة (individual numbers) بذاتها، مثل إِيجاد حاصل مجموع عناصر المصفوفة أو قيمة متوسط تلك العناصر أو قيمة أكبر عدد بها.
import textio.TextIO; public class ReverseInputNumbers { public static void main(String[] args) { int[] numbers; // مصفوفة لتخزين القيم المدخلة int count; // عدد الأعداد المخزنة فعليًا بالمصفوفة int num; // أحد الأعداد المدخلة من قبل المستخدم int i; // متغير حلقة for // مصفوفة أعداد صحيحة بطول 100 numbers = new int[100]; // لم يتم إدخال أي أعداد بعد count = 0; System.out.println("Enter up to 100 positive integers; enter 0 to end."); // اقرأ الأعداد وأضفها إلى المصفوفة while (true) { System.out.print("? "); num = TextIO.getlnInt(); // الصفر هو إشارة لانتهاء عملية الإدخال if (num <= 0) { break; } numbers[count] = num; // خزن العدد برقم الموضع count count++; // أزد العداد بمقدار واحد } System.out.println("\nYour numbers in reverse order are:\n"); for ( i = count - 1; i >= 0; i-- ) { System.out.println( numbers[i] ); } } // نهاية main(); } // نهاية الصنف ReverseInputNumbers
مِنْ المُهم أن تُدرِك الدور المزدوج الذي يؤديه المُتَغيِّر count. فبالإضافة إلى كَوْنه يَحمِل عدد العناصر التي أُدْخلت فعليًا إلى المصفوفة، فإنه أيضًا يُمثِل فهرس (index) المَوْضِع التالي المُتاح بالمصفوفة.
عندما يَحيِن موعد طباعة الأعداد الموجودة بالمصفوفة، يكون رقم المَوْضِع الأخير المُستخدَم فعليًا بالمصفوفة count - 1، ولذا تَطبَع حَلْقة التَكْرار for قيم عناصر المصفوفة بداية من رقم المَوْضِع count - 1، ونزولًا إلى المَوْضِع صفر. يُعدّ هذا مثالًا جيدًا لمعالجة عناصر مصفوفة ما بترتيب مُعاكِس (reverse order).
قد تتساءل، ماذا سيَحدُث بالبرنامج إذا حاول المُستخدِم إِدْخَال أكثر من ١٠٠ عدد؟ ستكون النتيجة حُدوث خطأ (error) يَتسبَّب بانهيار (crash) البرنامج؛ فعندما يُدْخِل المُستخدِم العدد رقم ١٠١، سيُحاول البرنامج تَخْزِين ذلك العدد بعنصر مصفوفة number[100]. لكن، في الواقع، هذا العنصر غَيْر موجود؛ حيث يُوجد فقط ١٠٠ عنصر بالمصفوفة، وفهرس آخر عنصر بها هو ٩٩، ولذلك ستؤدي محاولة اِستخدَام number[100] إلى حُدوث اِعتراض (exception) من النوع ArrayIndexOutOfBoundsException. تُعدّ الاعتراضات من هذا النوع مصدرًا شائعًا لحُدوث أخطاء وقت التَّنْفيذ (run-time errors) بالبرامج التي تَستخدِم المصفوفات.
المصفوفات ثنائية البعد (Two-dimensional)
تُعدّ المصفوفات التي تَعامَلنا معها حتى الآن أحادية البعد (one-dimensional)، مما يَعنِي أن المصفوفة تتكون من متتالية من العناصر، والتي يُمكِن تَخَيُّلها وكأنها مَوْضوعة على خط (line). تَتوفَّر أيضًا المصفوفات ثنائية البعد (two-dimensional)، والتي تُوضَع فيها العناصر داخل شبكة مستطيلة الشكل (rectangular grid). سنمر على هذا الموضوع باختصار هنا، ونعود إليه مُجددًا بالقسم ٧.٥.
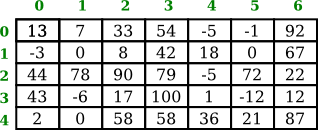
تُرتَّب عناصر المصفوفة ثنائية البعد (2D/two-dimensional array) بصورة صفوف (rows) وأعمدة (columns). على سبيل المثال، تتكون مصفوفة الأعداد الصحيحة ثنائية البعد (2D array of int) التالية من ٥ صفوف و ٧ أعمدة:
تتكون الشبكة ٥*٧ بالأعلى من ٣٥ عنصر. تُرقَّم الصفوف بالمصفوفة ثنائية البعد كالتالي: ٠، ١، ٢، …، وحتى عدد الصفوف ناقص واحد. بالمثل، تُرقَّم العواميد من ٠ وحتى عدد العواميد ناقص واحد. يُمكِن الولوج لأيّ عنصر مُفرد (individual element) بالمصفوفة من خلال رقمي الصف (row number) والعمود (column number) خاصته. (لا تبدو المصفوفة بذاكرة الحاسوب كالصورة المَعروضة بالأعلى، فهي مُجرَّد توضيح للبناء المنطقي [logical structure] للمصفوفة)
تُشبه صيغة (syntax) المصفوفات ثنائية البعد (two-dimensional arrays) بلغة الجافا نفس تلك الصيغة المُستخدَمة مع المصفوفات أحادية البعد (one-dimensional arrays)، باستثناء وجود فهرس (index) إِضافي؛ لأن الولوج لأيّ عنصر أَصبح يَتطلَّب كُلًا من رقمي الصف (row number) والعمود (column number). على سبيل المثال، إذا كانت A مصفوفة أعداد صحيحة (array of int) ثنائية البعد، فسيُشيِر A[3][2] إلى العنصر الموجود بالصف رقم ٣ والعمود رقم ٢، والذي يَحمِل العدد ١٧، كما هو موضح بالمصفوفة بالأعلى. كذلك، سيكون نوع مُتَغيِّر المصفوفة، في هذه الحالة، هو كلمة int متبوعة بزوجين من الأقواس المعقوفة (square brackets) الفارغة، أيّ int[][].
يمكنك كتابة التالي للتَّصْريح (declare) عن مُتَغيِّر مصفوفة (array variable)، بالإضافة إلى إِنشاء تلك المصفوفة:
int[][] A; A = new int[5][7];
يُنشِئ السطر الثاني مصفوفة ثنائية البعد (2D array) مُكوَّنة من ٥ صفوف و ٧ أعمدة. غالبًا ما تُستخدَم حَلْقات التَكْرار for المُتداخِلة (nested) لمعالجة المصفوفات ثنائية البعد. على سبيل المثال، تَطبَع الشيفرة التالية عناصر المصفوفة A:
int row, col; // متغيرات التحكم بالحلقة احدهما للصف والآخر للعمود for ( row = 0; row < 5; row++ ) { for ( col = 0; col < 7; col++ ) { System.out.printf( "%7d", A[row][col] ); } System.out.println(); }
يُمكِن أن يكون النوع الأساسي (base type) لمصفوفة ثنائية البعد أيّ شئ، أيّ أنك تستطيع إِنشاء مصفوفات ثنائية البعد من النوع العددي double، أو النوع String، وهكذا.
توجد عدة اِستخدَامات طبيعية للمصفوفات ثنائية البعد (2D arrays)، والتي تَكُون فيها الشبكة (grid) واضحة مرئيًا. فمثلًا، قد تُخزِن مصفوفة ثنائية البعد محتويات اللوحة (board) بألعاب مثل الشطرنج أو الدَّامَا (checkers). يُوظِّف مثال آخر، بالقسم الفرعي ٤.٧.٣، مصفوفة ثنائية البعد لحفظ ألوان شبكة (grid) مُكوَّنة من مربعات ملونة. يُمكِنك أيضًا تَوظِيف المصفوفات ثنائية البعد بمسائل لا تكون فيها الشبكة واضحة مرئيًا. فمثلًا، لنفْترِض وجود شركة تَملك ٢٥ مَخزنًا. تَحتفِظ الشركة ببيانات الأرباح التي كَسَبَها كل مَخزن شهريًا طوال عام ٢٠١٨. إذا كانت المخازن مُرقَّمة من ٠ إلى ٢٤، وكانت الشهور الاثنى عشر، أي من يناير ٢٠١٨ وحتى ديسمبر ٢٠١٨، مُرقَّمة من ٠ إلى ١١، فمِنْ ثَمَّ، يُمكِن تَخْزِين هذه البيانات بمصفوفة تَحمِل اسم profit، وتُنشَئ كالتالي:
double[][] profit; profit = new double[25][12];
يُمثِل المُتَغيِّر profit[3][2] قيمة أرباح المَخزن رقم ٣ بشهر مارس. بصورة أعم، يُمثِل المُتَغيِّر profit[storeNum][monthNum] قيمة أرباح المَخزن رقم storeNum بالشهر رقم monthNum (تذكر أن الترقيم يبدأ من صفر.)
لنفْترِض أن مصفوفة الأرباح profit ممتلئة بالبيانات بالفعل. وعليه، يمكن معالجة هذه البيانات بطرائق كثيرة شيقة. على سبيل المثال، يُمكِن حِسَاب الأرباح الكلية للشركة -جميع المَخازن طوال عام ٢٠١٨- بحِسَاب قيمة حاصل مجموع جميع عناصر المصفوفة، كالتالي:
double totalProfit; // الأرباح الكلية للشركة بعام 2018 int store, month; // متغيرات حَلقتي التكرار totalProfit = 0; for ( store = 0; store < 25; store++ ) { for ( month = 0; month < 12; month++ ) totalProfit += profit[store][month]; }
تحتاج أحيانًا إلى معالجة صف وحيد أو عمود وحيد بالمصفوفة، وليس المصفوفة بكاملها. على سبيل المثال، تستطيع اِستخدَام حَلْقة التَكْرار التالية لحِسَاب قيمة الأرباح الكلية للشركة بشهر ديسمبر، أيّ بالشهر رقم ١١:
double decemberProfit; int storeNum; decemberProfit = 0.0; for ( storeNum = 0; storeNum < 25; storeNum++ ) { decemberProfit += profit[storeNum][11]; }
قد تجد أن المصفوفات ثنائية البعد (two-dimensional array) مفيدة في بعض الأحيان، ولكنها عمومًا أقل شيوعًا من المصفوفات أحادية البعد (one-dimensional). وفي الواقع، تَسمَح لغة الجافا كذلك بمصفوفات ذات أبعاد أعلى (higher dimension)، ولكن يَنْدُر اِستخدَامها عمليًا.


تعليقات
إرسال تعليق