لقد تَعلَّمت، على مدار الفصلين السابقين، نوعية البرمجة المُستخدَمة أثناء كتابة برنامج فرعي وحيد (subroutine)، فيما أطلقنا عليه اسم "البرمجة في نطاق ضيق". سنُركز أكثر خلال الفصول المُتبقّية من الكتاب على بناء البرامج ضِمْن نطاق أوسع، ولكن ما يزال ما تَعلَّمته حتى الآن هو البذرة الأساسية والضرورية لكل ما ستَتَعرَّض له فيما بَعْد.
سنرى، في هذا القسم، كيف يُمكِن تطبيق ما قد تَعلَّمته خلال الفصول السابقة ضِمْن سياق برمجة واجهات المُستخدِم الرسومية (graphical user interface)، والتي تُعرَف اختصارًا باسم GUI، وهو سِّياق مُختلف نوعًا ما عما اعتدته من برامج الطرفيّة النصية. ستَعتمِد برمجة الواجهات الرسومية (GUI) سواء التي سنَتَعرَّض لها خلال هذا القسم أو خلال بقية الكتاب على منصة JavaFX، والتي تَضُمّ مجموعة من الأصناف (classes) المُستخدَمة لكتابة هذه النوعية من البرامج، أيّ أن جميع الأصناف (classes) المذكورة بهذا القسم هي جزء من منصة JavaFX، وبالتالي يَنبغي أن تقوم باستيرادها (import) إلى البرنامج حتى تَتَمكَّن من اِستخدَامها. اُنظر القسم ٢.٦ لمزيد من المعلومات عن تَصرِّيف (compiling) البرامج المُستخدِمة لمنصة JavaFX وكيفية تَشْغِيلها.
عند تَشْغِيل برامج واجهات المُستخدِم الرسومية (GUI)، ستُفتَح نافذة واحدة (window) أو أكثر على شاشة الحاسوب الخاصة بك. يُمكِنك، كمبرمج، التَحكُّم الكامل بما يَظهر على تلك النافذة، وكذلك بالكيفية التي يُمكِن للمُستخدِم التَفاعُل (interact) بها مع النافذة. سنَفْحَص خلال هذا القسم أمثلة بسيطة مثل طباعة بعض الأشكال البسيطة كالخطوط والمستطيلات على النافذة بدون أي تَفاعُل من المُستخدِم، فالنقطة المُهمّة، في الوقت الحالي، هو أن تتعرَّف على الطريقة التي تُستخدَم بها أساليب "البرمجة في نطاق ضيق" ضِمْن سياقات اخرى غَيْر برامج الطرفية المُعتمدة على النصوص، وسترى بنفسك أنه يمكن تطبيق نفس تلك الأساليب لكتابة أيّ برنامج فرعي (subroutine) وليس فقط البرنامج main.
رسم الأشكال
ستحتاج إلى أن تَكُون على دراية ببعض المفاهيم كالبكسل (pixels)، وأنظمة الإِحداثيَّات (coordinate systems)؛ كي يتَسَنَّى لك فهم الرسومات الحاسوبية (computer graphics)، ولذلك سنمر على بعض المفاهيم الأساسية سريعًا.
تتكون عامةً شاشة الحاسوب (computer screen) من مربعات صغيرة تُسمى البكسل (pixels)، مُرَتَّبة بصورة صفوف وعواميد، بدقة تَصِل عادةً إلى ١٠٠ بكسل لكل بُوصَة (pixels per inch). تَحتوِي الكثير من الشاشات حاليًا على عدد أكبر بكثير من البكسلات المَلْموسة (physical pixels) لكل بُوصَة، لدرجة أنه مِنْ المُحتمَل لبكسل منصة JavaFX أن يُشير إلى بكسل مَلْموس (physical pixel) بمثل هذه الشاشات عالية الدقة (high-resolution)، ولكنه على الأرجح يُشيِر إلى بكسل مَنطقي (logical pixel)، والتي هي وَحدة قياس تُعادِل ٠.٠١ بوصة تقريبًا.
لمّا كان باستطاعة الحاسوب التَحكُّم بلون البكسل، فإنه، في الواقع، يَرسِم (drawing) الأشكال عن طريق تَغْيِير ألوان البكسلات المُفردة (individual pixels). كل بكسل له زوج من الإِحداثيَّات (coordinates)، يُشار إليها عادة باسم الإِحداثيّ x والإِحداثيّ y، وتُستخدَم لتَحْدِيد المَوْضِع الأفقي (horizontal) والرأسي (vertical) للبكسل على الترتيب. عند الرسم بمساحة مستطيلية الشكل على الشاشة، تَكُون إِحداثيَّات البكسل بالرُكْن العُلوِي الأيسر (upper left corner) هي (٠،٠)، وبحيث تزداد قيمة الإِحداثيّ x من اليسار إلى اليمين، بينما تزداد قيمة الإِحداثيّ y من الأعلى إلى الأسفل. يُستخدَم البكسل لتَحْدِيد الأشكال وتَعرَيفها، فعلى سبيل المثال، يُعرَّف أيّ مستطيل من خلال الإِحداثيّ x والإِحداثيّ y بالرُكْن العُلوِي الأيسر للمستطيل، بالإضافة إلى كُلًا من عَرْضه (width)، وارتفاعه (height) بوَحدة البكسل.
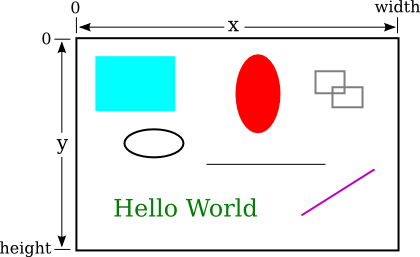
تَعرَض مساحة الرسم (drawing area) بالصورة التالية نطاق كلًا من الإِحداثيَّات x و y، ويُمثِل العَرْض والارتفاع بها حجم مساحة الرسم بوَحدة البكسل:
بفَرْض أن مساحة الرسم (drawing area) -بالأعلى- مُكوَّنة من ٨٠٠*٥٠٠ بكسل، سيكون المستطيل، الواقع بالجزء العُلوِي الأيسر من الصورة، تقريبًا بعَرْض ٢٠٠ بكسل وارتفاع ١٥٠ بكسل، كما يَقع الرُكْن العُلوِي الأيسر (upper left corner) للمستطيل بالإِحداثيَّات (٥٠،٥٠) تقريبيًا.
يَتمّ الرسم بلغة الجافا باِستخدَام كائن سِّياق رُسومي (graphics context) من النوع GraphicsContext. يَشتمِل هذا الكائن على بعض البرامج الفرعية (subroutines)، مثل برامج (routines) لرسم الأشكال البسيطة كالخطوط، والمستطيلات، والأشكال البيضاوية، والنصوص. (عندما يَظهر النص على الشاشة، يَرسِم الحاسوب حروف النص مثلما يَرسِم أيّ أشكال آخرى). بالإضافة إلى ذلك، يَشتمِل كائن السِّياق الرُسومي (graphics context) أيضًا على مجموعة من البيانات (data)، مثل نوع الخط المُختار حاليًا للرَسْم ولونه. (يُحدِّد نوع الخط كلًا من حجم وشكل الحروف). تَشتمِل بيانات كائن السِّياق أيضًا على سطح رسم (drawing surface)، وهو ما يَتمّ الرسم عليه، وفي حالتنا، سيكون سطح الرسم هو مساحة مُحتوَى النافذة بدون الحواف (border) وشريط العنوان (title bar)، ولكن تَتوفَّر أسطح رَسْم مختلفة يمكن الرَسْم عليها أيضًا.
تُوفِّر منصة JavaFX طريقتين لرسم الأشكال: إِمّا بمَلْئ الشكل (filling) أو بتَحْدِيد حوافه (stroking). مَلْئ الشكل (filling) هو ضَبْط لون كل بكسل بداخله، أمَا تَحْدِيد حواف الشكل (stroking) فهو ضَبْط لون البكسلات الواقعة بحوافه (border)، وهو ما يُشبه عملية سَحب قلم على طول حواف الشكل، وفي هذه الحالة، تُعدّ صفات القلم -كحجمه (width/size) أو ما إذا كان يَستخدِم خط صلب (solid line) أو مُتقطِّع (dashed line)- خاصيات (properties) ضِمْن كائن السِّياق الرُسومي (graphics context). يُخصِّص كائن السِّياق الرُسومي أيضًا لونين مُنفصلين، أحدهما لمَلْئ الأشكال (filling)، والآخر لتَحْدِيد حوافها (stroking). لاحظ اقتصار بعض الأشكال -كالخطوط- على طريقة تَحْدِيد الحواف فقط.
يُستخدَم مُتَغيِّر من النوع GraphicsContext لتَمثيِل السِّياق الرُسومي (graphics context)، ويَحمِل هذا المُتَغيِّر عادةً الاسم g. ليس هذا ضروريًا بالطبع، حيث يَتوقَف اسمه بالنهاية على المُبرمج. نَعرِض هنا بعض البرامج الفرعية (subroutines) المُتوفرة ضِمْن كائن السِّياق الرُسومي g. لاحظ أن كل قيم المُعامِلات العددية هي من النوع double:
البرنامج الفرعي
g.setFill(c): يَضبُط اللون المُستخدَم لمَلْئ الأشكال (filling)، حيث المُعامِلcهو كائن من الصَنْفColor. تَتوفَّر الكثير من الثوابت (constants) المُمثِلة للألوان القياسية (standard colors)، والتي يُمكِن اِستخدَامها كمُعامِل لهذا البرنامج الفرعي. تتراوح الألوان القياسية من الألوان الشائعة مثلColor.BLACKوColor.WHITEوColor.REDوColor.GREENوColor.BLUEوColor.YELLOW، إلى بعض الألوان الغريبة مثلColor.CORNFLOWERBLUE. (يُمكِنك أيضًا إِنشاء ألوان جديدة مُخصَّصة). على سبيل المثال، إذا أردت مَلْئ الأشكال باللون الأحمر، فإنك ستَستدعِي البرنامج الفرعيg.setFill(Color.RED);. لاحظ أن اللون المُخصَّص أثناء الاستدعاء سيُستخدَم لجميع عمليات المَلْئ التالية وحتى الاستدعاء التالي لنفس البرنامج الفرعي، أما الأشكال المَرسومة مُسْبَّقًا فلا تتأثر بهذا التَغْيِير.البرنامج الفرعي
g.setStroke(c): يَضبُط اللون المُستخدَم لتَحْدِيد حواف الأشكال (stroking)، ويَعمَل بصورة مشابهة للبرنامج الفرعيg.setFill.البرنامج الفرعي
g.setLineWidth(w): يَضبُط حجم القلم المُستخدَم خلال عمليات تَحْدِيد الحواف التالية (stroking). لاحظ أن المُعامِلwيَستخدِم وَحدة البكسل.البرنامج الفرعي
g.strokeLine(x1,y1,x2,y2): يَرسِم خطًا مُمتدًا من إِحداثيَّات نقطة البداية (x1,y1) وحتى إِحداثيَّات نقطة النهاية (x2,y2). يُرسَم الخط باللون الأسود وبحجم ١ بكسل افتراضيًا، ومع ذلك، يُمكِنك تَخْصِيص كلًا منهما باستدعاءg.setStroke()وg.setLineWidth() على الترتيب.البرنامج الفرعي
g.strokeRect(x,y,w,h): يَرسِم الحواف الخارجية (stroking) لمستطيل مع جوانبه الأفقية والرأسية، بحيث يَبعُد الرُكْن العُلوِي الأيسر (top-left corner) لهذا المستطيل مسافة قدرهاxبوَحدة البكسل عن الحافة اليسرى لمساحة الرسم (drawing area)، ومسافة قدرهاyبوَحدة البكسل عن حافتها العُلوِية. يُحدِّد كلًا من المُعامِلينwوhعَرْض المستطيل الأفقي وارتفاعه الرأسي بوَحدة البكسل على الترتيب. يُمكِن ضَبْط لون الخط المُستخدَم وحجمه باستدعاءg.setStroke()وg.setLineWidth() على الترتيب.البرنامج الفرعي
g.fillRect(x,y,w,h): يَعمَل بصورة مشابهة للبرنامج الفرعيg.strokeRect() باستثناء أنه يَملْئ المستطيل (filling) بدلًا من رسم حوافه الخارجية (stroking). اِستدعيg.setFillلضَبْط اللون المُستخدَم.البرنامج الفرعي
g.strokeOval(x,y,w,h): يَرسِم الحواف الخارجية لشكل بيضاوي. يُرسَم الشكل البيضاوي بحيث يَقع ضِمْن المستطيل الذي كان سيُرسَم في حالة استدعاءg.strokeRect(x,y,w,h)بنفس قيم المُعامِلات. لاحِظ أنه يُمكِنك اِستخدَام نفس القيمة لكُلًا من المُعامِلينwوhلرسم حواف دائرة.البرنامج الفرعي
g.fillOval(x,y,w,h): يَعمَل بصورة مشابهة للبرنامج الفرعيg.strokeOval() باستثناء أنه يَملْئ الشكل البيضاوي بدلًا من رَسْم حوافه الخارجية.
تُعدّ هذه البرامج الفرعية كافية لرَسْم بعض الصور باِستخدَام الجافا. لنبدأ بشئ بسيط مثل رَسْم عشرة خطوط متوازية، كالتالي:
نحتاج أولًا لمجموعة افتراضات هي كالتالي: سيكون طول الخطوط حوالي ٢٠٠ بكسل، والمسافة بين كل خط والخط الذي يَليه حوالي ١٠ بكسل، وأخيرًا، سنفْترِض أن نقطة بداية (start) أول خط تقع بالإِحداثيَّات (١٠٠،٥٠). الآن، كل ما نحتاج إليه لرَسْم خط هو استدعاء البرنامج الفرعي g.strokeLine(x1,y1,x2,y2) بقيم مُعامِلات مناسبة. نلاحِظ أن نقطة البداية (start) لجميع الخطوط لها نفس قيمة الإِحداثيّ x (x-coordinate) وتُساوِي ١٠٠، ومِنْ ثَمَّ، سنَستخدِم قيمة ثابتة تُساوِي ١٠٠ كقيمة للمُعامِل x1. لمّا كانت جميع الخطوط بطول ٢٠٠ بكسل، فإننا سنَستخدِم قيمة ثابتة تُساوِي ٣٠٠ كقيمة للمُعامِل x2. في المقابل، تَختلف إِحداثيَّات y (y-coordinates) بكل خط عن الخط الذي يَليه، ولكن يُمكِننا أن نرى أن قيمة الإِحداثيّ y بنقطتي البداية (start) والنهاية (end) لكل خط منها هو نفسه، وعليه، سنَستخدِم مُتَغيِّر وحيد لكُلًا من قيمتي y1 و y2، هو المُتَغيِّر y. الآن، أصبح أمر الاستدعاء لرَسْم أحد الخيوط كالتالي g.strokeLine(100,y,300,y). اِفْترَضنا قبلًا أن قيمة المُتَغيِّر y لأول خط هي ٥٠، ثم ستزداد تلك القيمة بمقدار ١٠ مع كل انتقال للخط التالي، مما يَعنِي أننا سنحتاج إلى التأكد من أن قيمة y تأخذ القيمة الصحيحة من متتالية الأعداد. يُمكِننا اِستخدَام حَلْقة تَكْرار for، كالتالي:
int y; // إحداثي y للخط int i; // المتغير المتحكم بالحلقة y = 50; // تبدأ y بالقيمة 50 لأول خط for ( i = 1; i <= 10; i++ ) { g.strokeLine( 100, y, 300, y ); y = y + 10; // أزد y بمقدار 10 قبل رسم الخط التالي }
نستطيع أيضًا اِستخدَام المُتَغيِّر y ذاته كمُتحكِّم بالحَلْقة (loop control variable). لاحِظ أن قيمة y للخط الأخير هي ١٤٠. انظر الشيفرة التالية:
int y; for ( y = 50; y <= 140; y = y + 10 ) g.strokeLine( 100, y, 300, y );
إذا أردت تلوين الخطوط باللون الأزرق، اِستدعي البرنامج الفرعي g.setStroke(Color.BLUE) قبل رَسْمها، حيث سيُستخدَم اللون الأسود افتراضيًا إذا قُمت برَسْمها دون ضَبْط اللون. أما إذا أردت أن يَكُون حجم تلك الخطوط ٣ بكسل، اِستدعي البرنامج الفرعي g.setLineWidth(3) قَبْل رَسْمها.
لننتقل إلى مثال أكثر تعقيدًا، فمثلًا، لنَرسِم عددًا كبيرًا من الدوائر بشكل عشوائي سواء فيما يَخُص مَوْضِعها (position) أو لونها. لمّا كنا على علم بعدد قليل من الألوان المُتوفرة، فإننا سنختار عشوائيًا واحدًا من الألوان التالية : الأحمر، والأخضر، والأزرق، والأصفر. سنستعمل تَعْليمَة switch بسيطة للاختيار، وذلك بطريقة شبيهة للمثال بالقسم الفرعي ٣.٦.٤:
switch ( (int)(4*Math.random()) ) { case 0: g.setFill( Color.RED ); break; case 1: g.setFill( Color.GREEN ); break; case 2: g.setFill( Color.BLUE ); break; case 3: g.setFill( Color.YELLOW ); break; }
لمّا كنا نريد للدوائر أن تكون عشوائية التَموْضع، فسنحتاج إلى اختيار مركز الدوائر (center of circles) بصورة عشوائية. بفَرْض أن عَرْض مساحة الرسم (drawing area) وارتفاعها مُعطيين من خلال المُتَغيِّرين width و height على الترتيب، فسينبغي للمَوْضِع الأفقي (horizontal position) للمركز أن يكون قيمة عشوائية تتراوح من القيمة ٠ وحتى width-1. بالمثل، يَنبغي للمَوْضِع الرأسي (vertical position) لمركز الدائرة أن يَكُون قيمة عشوائية تتراوح من القيمة ٠ وحتى height-1. أخيرًا، ما زِلنا بحاجة لتَحْدِيد حجم الدائرة. سنكتفي، في هذا المثال، باِستخدَام نصف قطر (radius) ثابت لجميع الدوائر مُساوِي للقيمة ٥٠ بكسل. تُرسَم الدائرة باِستخدَام التَعْليمَة g.fillOval(x,y,w,h)، لكن، في الواقع، لا يُمثِل المُعامِلان x و y، بهذا الأمر (command)، إِحداثيَّات مركز الدائرة؛ وإنما إِحداثيَّات الرُكْن العُلوِي الأيسر (upper left corner) للمستطيل المرسوم حول الدائرة، ولهذا سنحتاج إلى تَحرِيك مركز الدائرة بمسافة قدرها يُساوِي نصف قطر الدائرة أي ٥٠ بكسل؛ وذلك للحصول على قيم x و y المُناظِرة. في المقابل، يُمثِل المُعامِلان w و h عَرْض وارتفاع المستطيل على الترتيب، واللذين ستكون قيمتهما مُساوِية لضعف نصف قطر الدائرة أي ١٠٠ بكسل بهذا المثال. تُراعِي الشيفرة التالية جميع النقاط المذكورة بالأعلى، وتُستخدَم لرَسْم دائرة عشوائية واحدة:
centerX = (int)(width*Math.random()); centerY = (int)(height*Math.random()); g.fillOval( centerX - 50, centerY - 50, 100, 100 );
لاحِظ أن الشيفرة بالأعلى تُستدَعى بَعْد استدعاء الشيفرة المسئولة عن ضَبْط اللون. تبدو الصورة عامةً بشكل أفضل بَعْد تَحْدِيد حافة الدائرة (border) باللون الأسود (stroking)، ولذلك أضيفت الشيفرة التالية:
g.setStroke( Color.BLACK ); g.strokeOval( centerX - 50, centerY - 50, 100, 100 );
وأخيرًا، للحصول على عدد كبير من الدوائر، ضُمِّنت الشيفرة بالأعلى داخل حَلْقة تَكْرار for، ونُفِّذت ٥٠٠ مرة، فكانت الرسمة الناتجة عن البرنامج كالتالي:
الرسم داخل برنامج
كما تعلم، لا يُمكِن لأيّ شيفرة بلغة الجافا أن تكون مُستقلة بذاتها، فلابُدّ لها أن تُكتَب ضِمْن برنامج فرعي (subroutine)، والذي بدوره يَكُون مُعرَّفًا داخل صَنْف (class)، ولهذا تَعرِض الشيفرة التالية التَعرِيف الكامل لبرنامج فرعي (subroutine definition)، والذي يُستخدَم لرَسْم الصورة من المثال السابق :
public void drawPicture(GraphicsContext g, int width, int height) { g.setFill(Color.WHITE); g.fillRect(0, 0, width, height); // املأ لون الخلفية بالأبيض // As an example, draw a large number of colored disks. // To get a different picture, erase this code, and substitute your own. int centerX; // احداثي x لمركز القرص int centerY; // احداثي y لمركز القرص int colorChoice; // قيمة اللون العشوائي int count; // المتغير التحكم بالحلقة for (count = 0; count < 500; count++) { centerX = (int)(width*Math.random()); centerY = (int)(height*Math.random()); colorChoice = (int)(4*Math.random()); switch (colorChoice) { case 0: g.setFill(Color.RED); break; case 1: g.setFill(Color.GREEN); break; case 2: g.setFill(Color.BLUE); break; case 3: g.setFill(Color.YELLOW); break; } g.fillOval( centerX - 50, centerY - 50, 100, 100 ); g.setStroke(Color.BLACK); g.strokeOval( centerX - 50, centerY - 50, 100, 100 ); } } // نهاية drawPicture()
هذه هي المرة الأولى التي تَتعرَّض فيها لتَعرِيف برنامج فرعي (subroutine definition) -إلى جانب main()-. سنتناول هذا الموضوع تفصيليًا بالفصل التالي، ولكن سنَمر عليه سريعًا هنا، يُتيِح السَطْر الأول من التَعرِيف الولوج لبعض القيم التي يَحتاجها البرنامج الفرعي، وهي السِّياق الرُسومي g، وكلًا من عَرْض وارتفاع مساحة الرسم width و height. يَستقبِل البرنامج الفرعي هذه القيم من مصدر خارجي، ويستطيع اِستخدَامها. ما يَهمّ هنا هو أن تُدرِك أنه لكي تَرِسم شيئًا (يَقصِد الكاتب أن هذا هو هدف البرنامج الفرعي، فاِسم البرنامج الفرعي هو drawPicture)، فستحتاج فقط إلى كتابة مُحتوَى البرنامج الفرعي، مثلما تَكتُب مُحتوَى البرنامج main() عند كتابة برنامج (الهدف من main()).
يَنبغي لتَعرِيف البرنامج الفرعي (subroutine definition) أن يَكُون بالصَنْف (class) الذي يُعرِّف البرنامج، وهو في هذه الحالة الصَنْف SimpleGraphicsStarter. شَّغِل البرنامج -مُتاح بالكامل بالملف SimpleGraphicsStarter.java- لترى الرَسمة، كما يُمكِنك اِستخدَام هذا البرنامج كنقطة بداية لرَسْم الصور الخاصة بك.
لاحِظ أنك لن تَفهم كل الشيفرة المكتوبة بالبرنامج، لكن ما يزال بإمكانك التَعديل عليها، فلا حاجة إلى فهم الشيفرة بأكملها، كل ما قد يَعَنيك هو الشيفرة الموجودة بالبرنامج الفرعي drawPicture(). اِحذف تلك الشيفرة، وضَعْ مكانها شيفرة الرسوم خاصتك، وستَتمكَّن بعدها من عَرْض رسوماتك.
بالمناسبة، قد تُلاحِظ أن الكلمة static مُستخدَمة بتَعرِيف البرنامج الفرعي main()، بعكس البرنامج الفرعي drawPicture()، الذي لا يَستخدِمها، وهو ما يَعنِي أن البرنامج الفرعي drawPicture() موجود بكائن (object) وليس بصَنْف (class). تُعدّ البرامج الفرعية التي تَستخدِم الكلمة static بتَعرِيفعها ساكنة (static)، أما التي لا تَستخدِمها فتُعدّ غَيْر ساكنة (non-static). الفرق بينهما مُهِمّ، ولكنه ليس بالأمر الذي يَنبغي أن تَقْلَق حِياله في الوقت الحاضر؛ حيث سنتناوله تفصيليًا بالفصل الخامس على أية حال.
التحريكة (Animation)
يَعتمِد التَحرِيك الحاسوبي (computer animation) على متتالية من الصور المُنفصلة، يُطلَق على كُل منها اسم الإطار (frame). تُعرَض هذه الصور بشكل سريع واحدة تلو الآخرى، فإذا كان التَغْيِير بين كل صورة والصورة التي تَليها طفيفًا، ستبدو متتالية الصور وكأنها تَحرِيكة مُستمرة (continuous animation). يُمكِنك اِستخدَام المثال التوضيحي بالملف SimpleAnimationStarter.java كنقطة بداية، حيث يَحتوِي على البرنامج الفرعي drawFrame() المَسؤول عن رَسْم إطار (frame) وحيد ضِمْن تَحرِيكة (animation)، بالإضافة إلى ذلك، يُنفَّذ البرنامج الفرعي drawFrame() أتوماتيكيًا حوالي ٦٠ مرة بالثانية، مما يَضمَن استمرار عَرْض الأُطُر (frames)، أيّ أنك تستطيع إِنشاء تَحرِيكة (animation) بمُجرَّد إضافة الشيفرة إلى هذا البرنامج الفرعي. تستطيع تمييز المرة الحالية من التَّنْفيذ من خلال مُتَغيِّرين إضافيين -إلى جانب السِّياق الرُسومي وكُلًا من عَرْض وارتفاع مساحة الرسم- يَستقبِلهما البرنامج الفرعي، وهما frameNumber و elapsedSeconds؛ حيث يأخذ المُتَغيِّر frameNumber القيم ٠، ١، ٢، ٣، .. والتي تَزداد بمقدار الواحد مع كل اِستدعاء للبرنامج الفرعي، أمَا قيمة المُتَغيِّر elapsedSeconds فتُشيِر إلى عدد الثواني التي مَرَّت على تَّنْفيذ التَحرِيكة حتى الآن. إجمالًا، تَستطيع رَسْم صورة مختلفة في كل مرة يُستدَعى فيها البرنامج الفرعي (subroutine) بالاعتماد على قيمة أيًا من هذين المُتَغيِّرين.
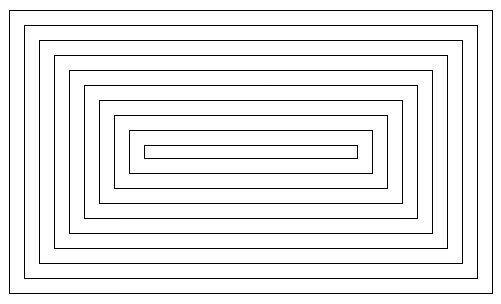
سنَرسِم بالمثال التالي مجموعة من المستطيلات المُتداخِلة (nested rectangles)، والتي ستنكمش باتجاه مركز الرَسْمة، مما سيُعطِي انطباعًا زائفًا بوجود حركة لا نهائية (infinite motion). تَعرِض الصورة التالية إِطارًا واحدًا من التَحرِيكة (animation):
لنُفكر كيف يُمكِن رَسْم مثل هذه الصورة. عامةً، يُمكِن اِستخدَام حَلْقة التَكْرار while لرَسْم المستطيلات، بحيث تبدأ أولًا برَسْم المستطيل الخارجي، ثُمَّ تنتقل إلى الداخل وهكذا. يَنبغي الآن أن نُفكر بالمُتَغيِّرات التي سنحتاج إليها خلال حَلْقة التَكْرار (loop)، وكذلك بالطريقة التي ستَتغَيَّر بها قيم تلك المُتَغيِّرات من تَكْرار (iteration) معين إلى التَكْرار الذي يليه. ستساعدنا الملاحظات التالية على مَعرِفة تلك المُتَغيِّرات، أولًا، مع كل تَكْرار، يكون المستطيل المرسوم أصغر منه في المرة السابقة، كما أنه يَتحرك للداخل قليلًا. يتركز عامةً الفارق بين أيّ مستطيلين على حجمهما وإِحداثيَّات (coordinates) رُكْنيهما اليساريين العُلوِيين (upper left corners)، ولهذا سنحتاج، أولًا، إلى مُتَغيِّرين لتَمثيِل كلًا من عَرْض المستطيل وارتفاعه، وهما المُتَغيِّران rectWidth و rectHeight على الترتيب. أما بالنسبة لإِحداثيَّات الرُكْن الأيسر العُلوِي x و y، فيُمكِن تَمثيِل كليهما بمُتَغيِّر وحيد للمستطيل الواحد، هو المُتَغيِّر inset؛ لأن قيمتهما مُتساوِية؛ حيث يَبعُد أيّ مستطيل عن حافتي مساحة الرسم (drawing area) بنفس مقدار المسافة. نُلاحِظ أنه مع كل تَكْرار، تَنقُص قيمة كلًا من عَرْض المستطيل rectWidth وارتفاعه rectHeight، بينما تزداد المسافة inset التي يَبعُدها المستطيل عن الحافتين. أخيرًا، تنتهي حَلْقة التَكْرار while عندما يُصبِح عَرْض المستطيل أو ارتفاعه أقل من أو يُساوِي الصفر. اُنظر خوارزمية رَسْم إِطار (frame) وحيد:
// املأ مساحة الرسم باللون الأبيض Fill the drawing area with white // اضبط قيمة inset المبدئية للمستطيل الأول الخارجي Set the amount of inset for the first rectangle // اضبط قيمة عرض وارتفاع المستطيل الأول الخارجي Set the width and height for the first rectangle // اضبط اللون المستخدم لتحديد الحواف إلى اللون الأسود Set the stroke color to black // طالما كان العرض والارتفاع أكبر من الصفر while the width and height are both greater than zero: // ارسم مستطيل باستخدام البرنامج الفرعي g.strokeRect draw a rectangle (using the g.strokeRect subroutine) // أزد قيمة inset حتى ينتقل المستطيل التالي إلى الداخل increase the inset (to move the next rectangle over and down) // انقص عرض وارتفاع المستطيل التالي حتى يصبح المستطيل التالي أصغر decrease the width and height (to make the next rectangle smaller)
ضُبطَت هذه النسخة من البرنامج بحيث يَبعُد كل مستطيل مسافة قدرها ١٥ بكسل عن المستطيل المُحيِط به، ولهذا فإن قيمة المُتَغيِّر inset تَزداد بمقدار ١٥ بكسل مع كل تَكْرار. في المقابل، يَتقَلص المستطيل حوالي ١٥ بكسل يمينًا ويسارًا، أيّ يَنقُص عَرْض المستطيل بمقدار ٣٠ بكسل. وبالمثل، يَنقُص ارتفاعه بمقدار ٣٠ بكسل مع كل تَكْرار ضِمْن الحلقة.
يَسهُل إعادة كتابة الخوارزمية بلغة الجافا، لكن تتبقَى فقط حاجتنا إلى معرفة القيم المبدئية للمُتَغيِّرات inset و width و height لأول مستطيل-(المستطيل الخارجي). لحساب ذلك، سنُفكر في حقيقة كَوْن الصورة متحركة (animated)، أي يَعتمِد ما نَرسِمه بطريقة ما على رقم الإِطار (frame number) الحالي. لمّا كان الرُكْن الأيسر العُلوِي (top-left corner) للمستطيل الخارجي يتحرك للأسفل وللداخل من أيّ إِطار إلى الإِطار الذي يَليه، فإن قيمة المُتَغيِّر inset المبدئية تزداد مع كل إِطار. قد تُفكر إذًا بضَبْط قيمة المُتَغيِّر inset المبدئية إلى القيمة ٠ بالإِطار رقم ٠، وإلى القيمة ١ بالإطار رقم ١ وهكذا. للأسف، لن يكون هذا صالحًا إلى الأبد؛ فعندما تَصِل التحريكة للإِطار ١٥، يَنبغِي أن يَظهر مستطيل خارجي جديد بمساحة الرَسْم (drawing area)، هو في الواقع ليس جديدًا، وإنما أُعيد فقط ضَبْط قيمة المُتَغيِّر inset المبدئية إلى القيمة ٠. إجمالًا، يَنبغِي لقيمة المُتَغيِّر inset أن تأخذ القيم ٠، ١، ٢، ٣،… حتى تَصِل إلى القيمة ١٤، لتُعاد الكَرَّة من جديد، وهو ما يُمكِن إنجازه باِستخدَام الشيفرة التالية:
inset = frameNumber % 15;
لاحِظ أن المستطيل يَملأ مساحة الرسم باستثناء حافة (border) تُحيِط به، عَرْضها يُساوِي قيمة المُتَغيِّر inset، أي بعبارة آخرى، عَرْض المستطيل هو عَرْض مساحة الرسم مطروحًا منه ضعف قيمة المُتَغيِّر inset، وبالمثل لارتفاعه. انظر شيفرة البرنامج الفرعي drawFrame() كاملة بالأسفل والمسئولة عن تَحرِيك المستطيل:
public void drawFrame(GraphicsContext g, int frameNumber, double elapsedSeconds, int width, int height) { g.setFill(Color.WHITE); g.fillRect(0,0,width,height); // املأ مساحة الرسم باللون الأبيض // المسافة بين بين المستطيل الخارجي ومساحة الرسم double inset; double rectWidth, rectHeight; // عرض وطول أحد المستطيلات // اضبط اللون المستخدم لرسم حواف المستطيل g.setStroke(Color.BLACK); // إضافة القيمة 0.5 هو أسلوب للحصول على صورة أكثر وضوحًا inset = frameNumber % 15 + 0.5; rectWidth = width - 2*inset; rectHeight = height - 2*inset; while (rectWidth >= 0 && rectHeight >= 0) { g.strokeRect(inset, inset, rectWidth, rectHeight); inset += 15; // تبعد المستطيلات عن بعضها بمقدار 15 بكسل rectWidth -= 30; rectHeight -= 30; } }
البرنامج مُتاح بالكامل بالملف MovingRects.java. يُمكِنك أيضًا الإِطلاع على مثال توضيحي آخر للتحريك (animation) بالملف RandomCircles.java، والذي يُضيِف قرصًا ملونًا (colored disk) بشكل عشوائي مع كل إِطار جديد. سيُظهِر لك هذا المثال أن صورة الإِطار لا تُحذَف تلقائيًا قبل إِعادة رسم الإِطار التالي.




تعليقات
إرسال تعليق